图中
从上述定义可以看出,无穷小是一个变化过程。

上图表示,无穷小可以比较趋向0的速度,但不可以比较大小,因为无穷小只有一个。所谓同一过程,比如,在相同的x趋于0的过程中,lim(x^2/x)=0。就说x^2是比x的高阶无穷小,其实就是x^2趋于0的速度比x趋于0的速度更快。

等价无穷小其实就是趋向0的速度一致。

上图表示,两个无穷小如果等价,则只是相差一个高阶无穷小。
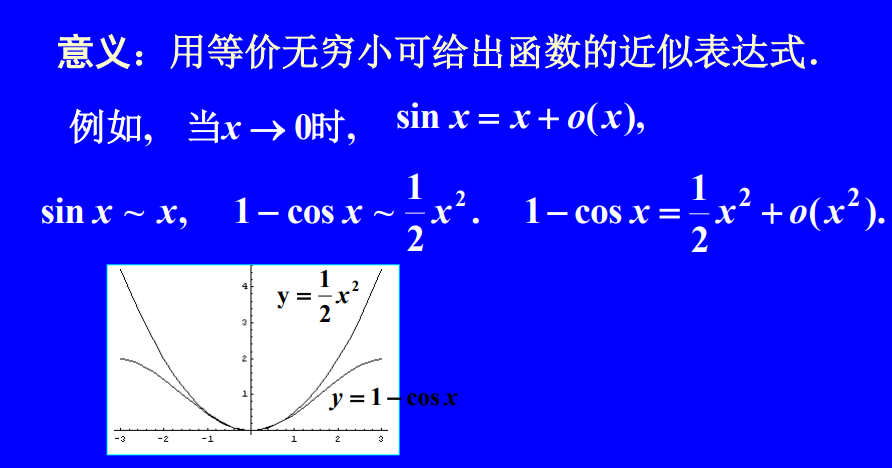
等价无穷小可以用于近似计算。
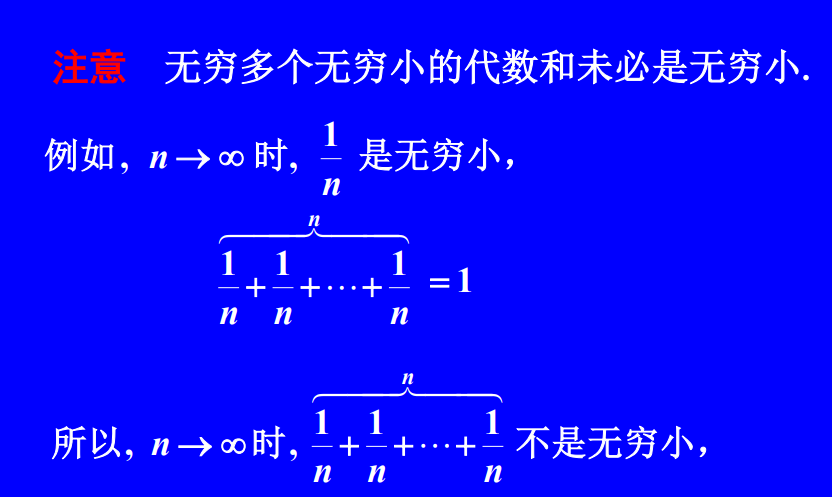
图1
上图表示,无穷多个无穷小之和不一定还是无穷小。而是有可能变成一个数字。
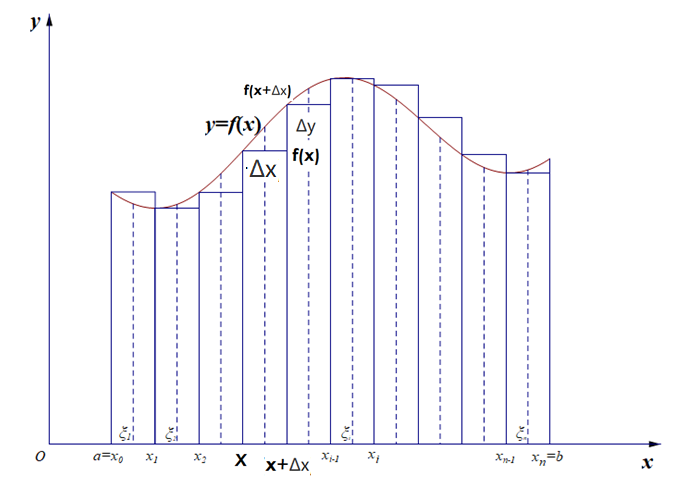
图2
上图是关于积分分割的说明。将x点的曲边梯形移到下面:
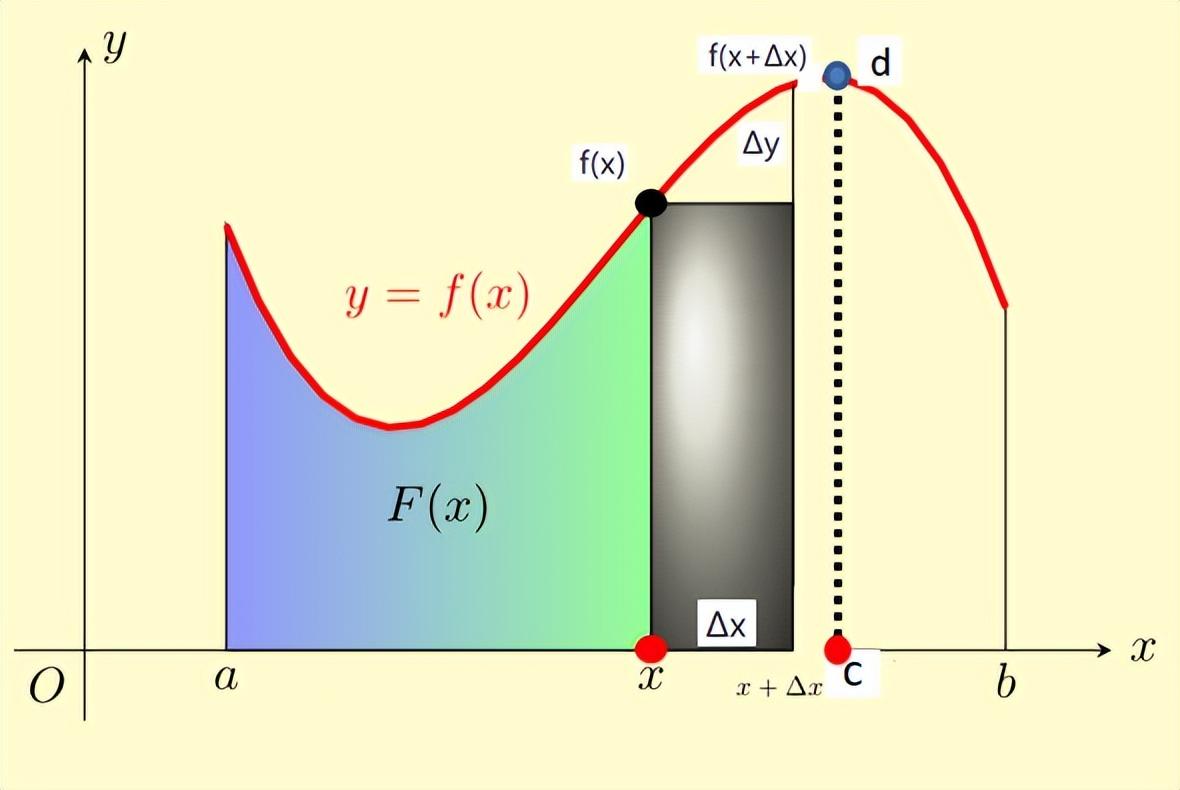
假设点c是和点x任意相邻的点,而Δx就是无穷小。关于无穷小的理解,作者在《数轴是一根连续的直线吗》一文中进行了详细解释。图中与点c相对应的点d是与点f(x)任意相邻的点。按照无穷小的定义,Δx是已经小到了无法用任何数字表示的程度。为了表示Δx不是一个数字的想法,上图中点c与位置x+Δx之间故意断开,表示点c是点x最相邻的那个数字,注意,点c可以任意。
同样,与点c相对应的点d采取了同样的方法,表示曲线上的点f(x)到f(x+Δx)之间的那段弧也不是一个数字。因为Δy= f(x+Δx)- f(x)也是一个无穷小,所以曲边梯形和矩形的面积之间就相差一个三角形的面积:1/2ΔxΔy,这个面积是一个高阶无穷小。矩形面积f(x)Δx是一个无穷小。只要是无穷小或者是高阶无穷小,就无法用数字表示出来。比如1+Δx只能等于1,因为Δx不是数字,所以1+Δx=1不是近似,而是精确相等。
按照图1,无穷多个无穷小之和不一定还是无穷小,而是有可能变成一个数字。这一结果表明,无穷小与一个具体的数字之间存在一个鸿沟,需要无穷多个无穷小才能跨越。同样,高阶无穷小和无穷小之间也存在鸿沟,无穷多个高阶无穷小不一定还是高阶无穷小,但最多能变成无穷小,但无穷小却还不是一个数字。
通过以上分析,图2中的曲边梯形面积和梯形面积之间略去的无穷多个三角形面积之和即高阶无穷小,最多相当于略去了一个无穷小,所以不会影响到积分的值是精确值这个结论。




