
三角函数是高中数学非常重要的一个模块,从近3年全国卷的高考真题发现,至少会有2-3道会出现,而且还可能出现在大题中,2022年的真题卷就是一道大题。
尽管卷子不同,但都会考查三角函数,只是考察的内容不一样,有的考察三角函数的化简、有的考察角度的计算、有的考察函数的性质、还有的考察边角的换算,今天我们就来总结下三角函数有哪些技巧可以使用,帮助我们快速做题!
1.化简公式
三角函数的化简公式很多,包括和差角公式、倍角公式以及降次公式,而记住了和差角公式就相当于记住了倍角公式,这点是一定要会运用的,不然你需要多记很多公式。而在考试中,重点考察的不是基础公式的换算,而是多项或者多次公式的化简和计算,这就需要大家记住3个核心的降次公式:
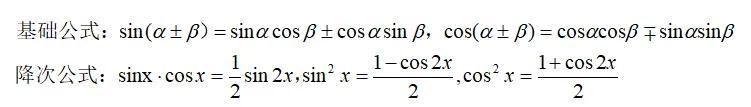
虽然降次公式可以通过基础公式换算得到,但在考试中直接运用可以大大节省做题时间,是非常关键的化简公式。
2.辅助角公式
辅助角公式是大部分三角函数计算会用到的公式,基础公式大家其实都知道,最难的是如何计算化简的度数,这里给大家最实用的技巧就是比系数定度数:

3.系数迁移法
三角函数最常见的就是变形,有那么一类题型完全不用公式换算就可以写答案:

本质上就是利用正切和差价角公式进行换算而来,但如果考试遇到相同的题型,就可以快速写答案了。
4.齐次计算法
经常会碰到有分式但次数不一致,甚至没有分数的,这类题型那么做?
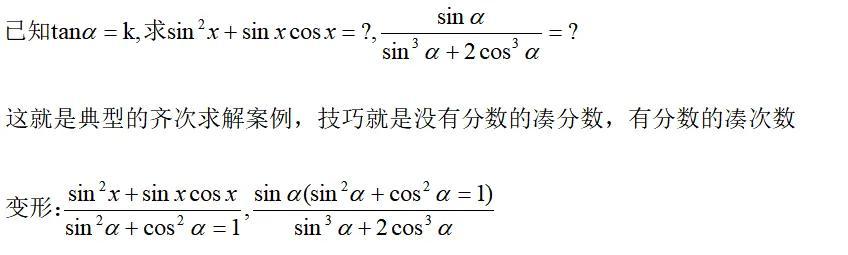
5.互补互余定理
诱导公式其实是非常有用的,本质上是周期的变换,大家最为熟知的就是“奇变偶不变,符号看象限”,在之前的发文中我有提到“数字7”的记忆法,这当然是记住全部的公式,但是对于一些普遍的情况,我们完全可以用更快的技巧来进行转换,我们把它称之为“互补互余定理”:

6.单调性求解
函数单调性是常考的知识点之一,做这类题只要把握住一点,不管形式怎么变,要记住最基础的形式和最基础的增减区间,整体代入就行。

7.对称性求解
三角函数对称求解无非就是对称中心和对称轴两种,和单调求解一个逻辑,再复杂的函数都是建立在最基础的形式上进行求解:

8.奇偶性求解
奇偶性求解有点类似化简的意思,因为往往题目给的不是直接能看出来奇偶性,而是需要进一步化简得到,如果能化简到f(x)=-f(-x),那么就是奇函数,化简到f(x)=f(-x),那就是偶函数。当然这是对所有函数如此,而三角函数有更快的技巧:

9.正弦定理
一般在三角形中,涉及到求边、求角或者求面积的,都会用到正余弦定理,核心还是边角转换的问题,如果左右式子在齐次的情况下,建议直接用边替换,因为已经齐次,如果不能约分是很难解出来的,如果没有齐次,先进行齐次操作。
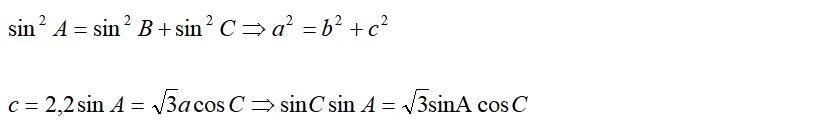
10.余弦定理
余弦定理比正弦定理稍微复杂一些,但核心也是边角转换的问题,在实际解题的过程中优先把角换成边,能更快地提高做题效率:

三角函数所有能快速提高做题效率的技巧都在这里了,小伙伴们用起来吧!

