六下数学:圆柱与圆锥的构成、特点与计算
学习是一个对自己的认知不断刷新的过程。
圆柱和圆锥的对比
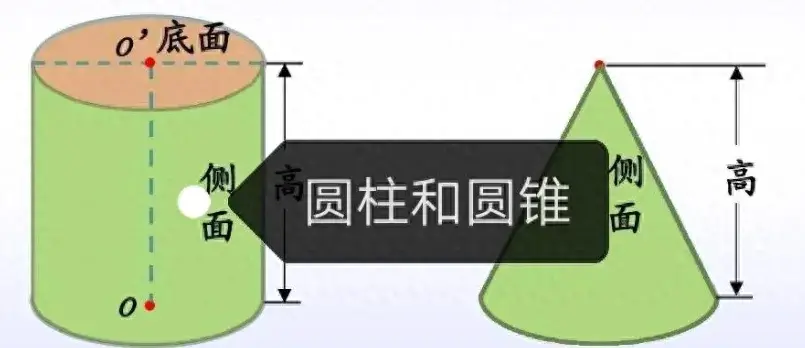
上小学之后,我们就逐渐的知道了"点的运动形成线,线的运动形成面,面的运动形成体″,“点、线、面、体”之间的关系,可以简记为“点动成线,线动成面,面动成体”。
1、圆柱
将一个长方形以其中的一条边为轴旋转一周所形成的几何体就是圆柱。
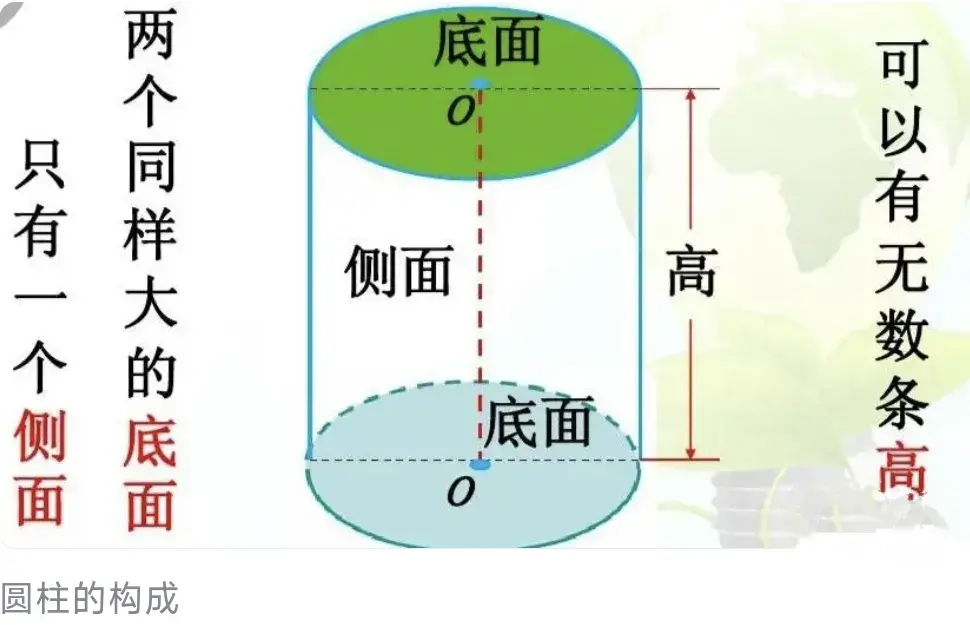
圆柱的构成
圆柱是由2个大小相同的圆面(上、下底面)和1个曲面(侧面)围成的,圆柱上下粗细均匀,上下底面间的距离叫作圆柱的高。
圆柱具有如下特征
①圆柱有两个底面和一个侧面;
②两个底面是完全相同的圆,侧面是一个曲面;
③圆柱有无数条高,所有的高都相等;
④圆柱的上、下底面平行;
⑤把圆柱的侧面沿某一直线展开可以得到一个矩形或平行四边形;
⑥圆柱侧面展开图的底是圆柱底面圆的周长,高是圆柱的高;
2、圆锥
以直角三角形的一条直角边为轴旋转一周所是形成的几何体就是圆锥。
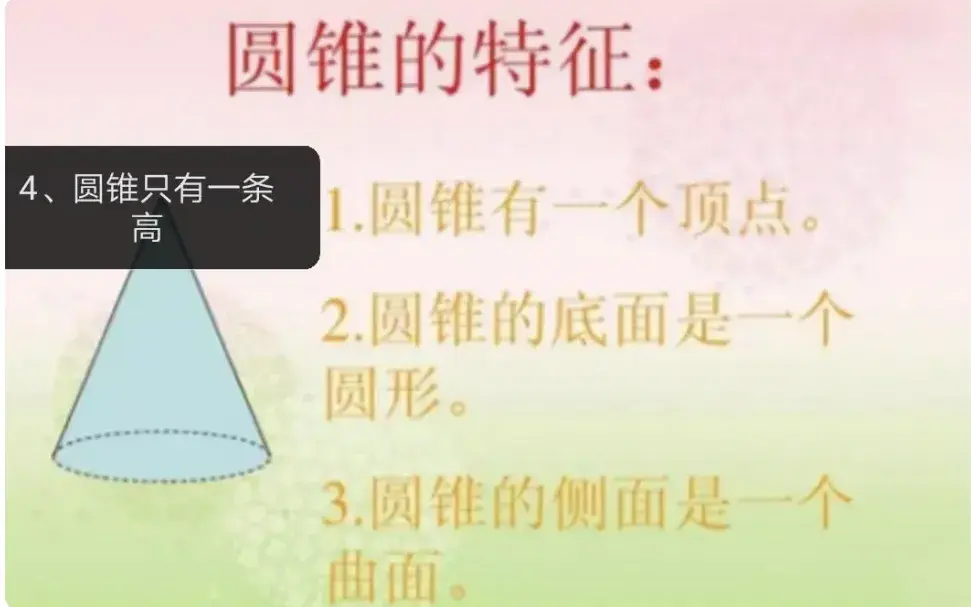
圆锥由1个圆面(底面)和1个曲面围成的。
圆锥的顶点到底面圆心的距离是圆锥的高。
圆锥的特征
①圆锥有一个底面和一个侧面;
②圆锥的底面是一个圆,侧面是一个曲面;
③圆锥只有一条高;
④圆锥的侧面展开是一个扇形。
3、圆柱和圆锥的切面
①把圆柱平行于底面横切,切面是大小相同的圆,叫横截面;
把圆柱沿底面直径纵切,切面是大小相同的长方形,叫圆柱的轴截面。
②把圆锥沿平行于底面的方向横切,每个切面是圆,但大小不同;
把圆锥沿顶点到底面圆心的直线纵切,切面是大小相同的等腰三角形。
4、圆柱的表面积
①圆柱的底面积:圆柱底面圆的面积,S底=2πr²;
②圆柱的侧面积:圆柱侧面(曲面)的面积,S侧=2πrh;
③S表=S底+S侧
5、圆柱和圆锥的体积
把一个圆柱沿半径切开,再拼成一个近似的长方体,则这个长方体的长近似等于圆柱底面周长的一半、宽等于底面圆的半径、高等于圆柱的高。因为长方体的体积等于:长×宽×高,所以圆柱的体积等于πr²h。
①圆柱的体积=底面积×高,用字母表示是V=Sh或V=πr²h;
②圆锥的体积=底面积×高锥÷3,用字母表示是V=Sh/3或V=πr²h/3。
6、圆锥的体积是与它等底等高的圆柱体积的三分之一。
在对圆柱的表面积进行求解时,一定要注意该圆柱的表面积中要求几个底面积:如常用的水桶、广场的立柱等,在计算表面积时只需计算一个表面积即可;而烟囱、排水(气)管、房屋(走廊)的立柱等,在计算表面积时只需计算侧面积,而不算入底面积。
计算圆锥的体积的时候千万别忘记除以3(或乘三分之一)。
圆柱切拼成近似的长方体后,体积不变,表面积变大,多出了一个轴截面的面积。




